профилирование

В очередной раз предлагаю потестировать Release Candidate свежего RawDigger:

• RawDigger-0.9.15-RC1-RU-Setup.exe - Windows, 32 бита.
• RawDigger-0.9.15-RC1-x64-RU-Setup.exe - Windows, x64
• RawDigger-0.9.15-RC1-RU.dmg - Mac, 32/64 бита

В версии 0.9.14 в RawDigger была добавлена удобная работа с цветовыми шкалами, но результат этой работы выводился в виде усредненных RAW-значений: в диапазоне значений камеры, без баланса белого, без гамма-коррекции. Как следствие, для нормального использования в программах профилирования эти данные приходилось предварительно обрабатывать в Excel или подобных программах: накладывать ББ, масштабировать, гамма-корректировать.

Версия 0.9.15 исправляет этот недостаток, теперь можно получить CGATS-файлы, пригодные для прямого скармливания в Profile Maker, Argyll и подобные программы.

Кроме этого, 0.9.15 умеет корректировать неравномерность освещения мишени.

Подробности:

Навеяно вот этим вот обсуждением, пожалуй запишу.

Абстрагируясь от профилей камер, давайте представим себе профиль принтера.

К примеру, Monaco Profiler с удовольствием сделает вам цветовой профиль с таблицами 33x33x33. То бишь почти 108 тысяч коэффициентов (+тоновые кривые). Круто, да.

А на вход ему при этом подадут ну, скажем, 1728 патчей (12 в кубе). Так как жрет он не спектральные данные, а простой рабоче-крестьянский XYZ, то это будет примерно 5200 значений.

Допустим, даже, мы введем еще ограничений: на гладкость интеполяционных функций, на знак третьей производной, ну придумаем еще. Ну еще десяток ограничений на точку (три на одно входное значение). Ну значит будет порядка 20 тыс. входных параметров.

Сколько можно построить интерполяционных функций, которые бы точно проходили через входные данные (dE -- нулевая) с учетом прочих ограничений? Имея в руках сотню тысяч параметров и 20 тысяч ограничений? Согласно общей теории всего - чуть меньше, чем дохрена. И они могут очень сильно отличаться в тех точках, где нет эксперимента. Но профиль - это модель (цветовоспроизведения) устройства, не может быть много сильно разных моделей.

Про то, с чего стартовали мои исходные раздумья (см. ссылку в начале), когда дополнительные данные получаются просто линейной комбинацией имеющихся, я и вовсе не говорю.

Я клоню к тому, что вижу в имеющемся подходе тупик: маленькие профили (с маленькой таблицей) дают плохую точность, это все знают из опыта. Большие профили (33x33x33) - основаны на выдуманных данных, а снабдить их невыдуманными данными, скажем промерять не пару тысяч патчей, а тысяч тридцать - невозможно на практике, слишком трудоемко.

В нормальной естественной науке вышеописанный тупик обычно является признаком несовершенства модели, приходится придумывать эпициклы высших порядков. Сдается мне, что в цветовой науке, в том виде, как ее видит ICC (со своими спецификациями) - подобная же хрень.

P.S. То что мишени для тех же принтеров генерируются, как правило, путем равномерной расстановки точек по всему пространству координат - отдельная печальная песня.

Несмотря на то, что существует некое подобие консенсуса, дескать у сенсоров Foveon все с цветами относительно неплохо, а если приложить специальный фильтр, то вообще все станет шоколадно, действительность оказалась гораздо хуже.

Второй день рассматриваю на мониторе разные колорчекеры, снятые разными сигмами и весь в печали. Независимо от используемого конвертора, никакого счастья нету.

На картинке - два результата конверсии Адобом (другие конверторы - дают другие результаты, но интегрально не лучше), две Сигмы (DP2 и SD14) и один 5DmkII. Попробуйте угадать где что.

Наиболее показателен, конечно, темно-красный патч C3, который правильный у Кэнона и совершенно разным способом неправильный у двух сигм. Но вообще, со всеми красно-оранжевыми цветами беда, да и с E3 тоже не подарок, да и вообще... SD9, кстати, еще хуже, там C2 и C3 вообще почти сливаются.

Нет, я понимаю, что счастье должно быть достижимо со специальным фильтром, но это теория такая, а на практике таких фильтров не существует.

Подумываю, что если из LibRaw дропнуть поддержку Foveon, то большой беды не будет, снимающих на *такие* камеры мне не жалко, а проблем оная поддержка создает несообразно много.

Несмотря на подразумеваемую "стандартность" ColorChecker, жизнь богаче. На картинке выше показана теоретическая разница между "Стандартным ColorChecker" (спектральные данные взяты из поставки Gretag/X-Rite ProfileMaker 5.0.8) и обсуждавшимся раньше ColorChecker Passport (спектральные данные из поставки программы Color Checker Passport, в версиях 1.0 и 1.0.1 они одинаковые). Расчет сделан Measure Tool из PM 5.0.8.

Тормоза на таможне счастливо завершились и ColorChecker Passport до меня счастливо добрался.

Имею сказать:

1. Если вы сторонник таскания ColorChecker на природу (и вообще на выезд), то эта штука как раз для вас: отличный форм-фактор (как паспорт в обложке), 100 граммов веса. Всяко лучше, чем ColorChecker Mini вставлять в коробку от DVD (хотя по данной ссылке у мужика самопальный): компактнее, жестче.

2. Часть, предназначенная для тонкой настройки баланса белого (верхняя половинка на фото) мне очень понравилась. И идея хорошая и реализация хорошая и пользоваться удобно.

3. ColorChecker (нижняя половинка разворота) - он ColorChecker и есть. Я свой пока не проверял, промеряю со временем, сравню со спектральным референсом (идет в комплекте софта), расскажу. Спектрального референса верхней половинки в поставке софта нет, при расчете профиля он не используется.

4. Второй разворот (их два т.к. "паспорт" кроме обложки содержит одну страничку) не такой прикольный, там карта для установки баланса белого (не очень нужная с учетом пункта 2) и напоминание о том, что производитель рекомендует заменять данный девайс раз в два года. Конечно, вместо надписи хотелось бы видеть каких-то других ништяков, более полезных, например серую карту (18%). Придется свою изрезать и туда вклеить.

О консенсусе

Несмотря на мой скепсис в отношении цветовой науки и любви потоптаться по святому, прикладную задачу копирования изображений я считал решенной (как минимум, в простых случаях).

Ну вот есть файл (RGB), к нему прилагается профиль (ICC), следует ожидать что на одном и том же устройстве (LCD мониторе, чтобы быть конкретным) он при включенном Color Engine отобразится более-менее разумно и одинаково.

Естественно, предполагается что все необходимые условия соблюдены: монитор отпрофилирован, показываемые цветовые данные привязаны к цвету (снабжены профилем), условия наблюдения постоянные, программа показа розумиет ICC, наливай да пей бери и выводи.

Конечно, жизнь несколько богаче и 2.5 года назад я уже исследовал проблему точности CMM (Color Management Module) и написал про это серию статей. Но я наблюдал в эксперименте разумные ошибки - 5-6, а для хороших CMM и 8 бит данных сохранялись, отклонения от смены CMM в худшем случае были заметны глазом, но не были фатальными.

Однако свежее письмо в Colorsync users и прилагавшийся к нему файлик заставили пересмотреть вышеописанное мнение. Спасибо добрым людям, что обратили внимание, не дали пройти мимо.

Да, на картинке слева вы видите кусочек из этого файла, показанный на одном и том же мониторе, с одним и тем же профилем монитора, одним и тем же профилем при цветовых данных файла, одной и той же программой (Adobe Photoshop) с одними и теми же настройками за исключением одной....

Вот этот вот комментарий, как мне кажется, заслужил отдельного обсуждения.

В самом деле, имеет место некий фенОмен (который виден, например, по dE т.е. инструментально):

• C одной стороны, цифровые камеры в светах (но до начала блюминга) - высоколинейны. Т.е. отпрофилировав их в среднем тоне мы вправе ожидать приличных цветов и в светах.
• C другой стороны, практика это опровергает, если снять цветовую шкалу +2 (без всяких вылетов) и наложить профиль камеры, то цвет уползет достаточно сильно (по меньшей мере, dE вырастет в разы)

Я тут вижу несколько соображений:

• Во-первых, блюминг. И, наоборот, всякие антиблюминговые решения, которые должны характеристическую кривую загибать.
• Во-вторых, всякие игры RAW-конвертеров (которые тоже характеристическую кривую загибают).
• В-третьих, следующий интересный эффект:
  1. Давайте представим себе профилировочную таблицу, вроде ColorChecker SG. Вот на ней есть зеленый патч E9, который на 1.5-2 стопа (на глазок) ниже среднесерого.
  2. Уровень красного в этом зеленом будет еще на пару стопов ниже (красного в нем мало), потом у красного канала чувствительность на стоп-полтора хуже т.е. красным мы попадем куда-то в -5 от среднего тона (или -8 от самых светов).
     Это, на минуточку, вообще на пределе какого-то сигнала в красном.
  3. Но красный канал нужен, чтобы отличить сине-зеленый от зелено-синего т.е. в этом месте профиля красный будет с очень большим весом (т.к. сам сигнал - маленький).
  4. Но красный - зашумлен, в рассматриваемом месте он уже сильно нелинеен (по причине шума)
• Собственно, вот: профиль для таких "предельных" цветов будет как-то компенсировать нелинейность слабых каналов, а если мы переедем на 3 стопа вверх - то перекомпенсировать (ибо на три стопа вверх в красном канале уже все отлично).

Такие дела.

В качестве алаверды к предыдущему посту имею сообщить, что хвалимый многими модуль дисплейной калибровки Argyll CMS мне не понравился:

• Задача-максимум: добиться одинакового визуального воспроизведения нейтральных плашек на двух мониторах не достигнута. Формально dE меньше единицы, но реально глаз видит разницу (которую можно устранить кривой в зеленом, но удобных средств редактирования LUT монитора у меня под рукой не было).
• Задача-минимум, собственно калибровка и профилирование, выполняются относительно неплохо, но калибровка идет средствами LUT видеокарты (т.е. 8-битной таблицы на DVI), точность работы средств, пищущих в LUT монитора - сильно выше (это видно при рассмотрении серого ступенчатого клина). Матричные профили имени Argyll мне при этом вполне нравятся, табличные - не нравятся.
• Использовать сам Argyll (коммандлайновые утилиты) необычайно мучительно, GUI сильно упрощает процесс. dispcalGUI задачу управления вполне решает.

С учетом вышесказанного, остался жить с basICColor.

В процессе этих упражнений, пронаблюдал эффект с потерей точности уже в CMM-engine (в фотошопе), который легко воспроизводится (и как только я его объяснил в уме, он перестал быть неожиданным):

• Калибровка и рабочий профиль у меня совпадают по точке белого (D50) и тоновой кривой (L*).
• Берем ступенчатый серый клин (я использую мишень от Norman Koren) в пространстве sRGB (D65 и степенная гамма-кривая), выводим фотошопом на экран, получаем (видимую) разноцветность по патчам.
• Image->Convert to RGB -> Beta-Lstar (рабочий профиль) - разноцветность патчей пропадает.

Эффект проявляется только для табличных (LUT) профилей и связан, естественно, с ошибками интерполяции содержащихся там таблиц (при построении условного device-link профиля пространство файла-пространство монитора). Для матричных профилей такой пересчет интерполяции не требует и, соответственно, ошибок не создает.

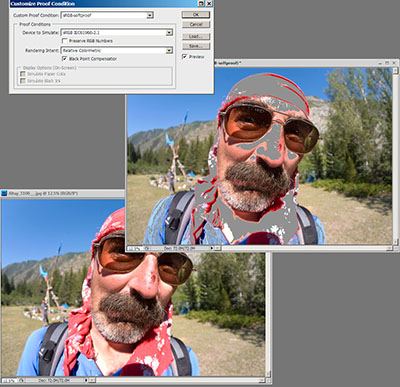Проект LibRaw стал настоящим — у нас завелся живой форумный тролль. Как от многих таких троллей, от него есть и некоторая польза: если кормить его вдумчиво, то можно заодно разобраться с какими-то вещами, до которых не доходили руки. В данном конкретном случае я разобрался с мониторным softproof (т.е. эмуляцией одного монитора на другом) и с пользой от этой техники для обработки изображений:

• поиск невидимых (искаженных) цветов на собственных картинках;
• оценка того, как изображение будет выглядеть на чужом мониторе (в том числе и в приложении, которое ничего не знает про профили и ICC).

Все эти вещи - интуитивно понятны, но их систематизация оказалась полезной и выродилась в отдельный текст:

Мониторный Softproof и Gamut Warning в Adobe Photoshop
...мониторный софтпруф может быть полезен тем, кто публикуется на фото-сайтах и подобным электронным образом, особенно для тех, кто обзавелся монитором с расширенным охватом и/или использует в качестве рабочего пространства - RGB пространство с охватом, много большим чем мониторный (например, Adobe RGB на обычном мониторе).
Помимо этого, вполне возможна ситуация, когда монитор не способен отобразить все цвета изображения - и это надо вовремя детектировать.