Вынос мозга тилт-шифтом: "гиперфокальное" расстояние

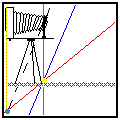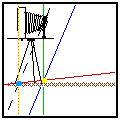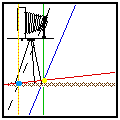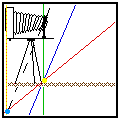
На картинке изображен процесс фотодрочерства, если кто вдруг не понял.

Моя предыдущая попытка вынести фотографам мозг полностью удалась. Мозг вынесен до такой степени, что комментариев практически не поступило, хотя я точно знаю, что тилт-шифты (включая и рассмотренный 24-мм) используют многие из читателей и в теории эти таблицы должны быть им интересны, хотя они еще и не понимают как.

В личных беседах я получил однозначную реакцию, сводящуюся к многа букаф, ниасилил.

Уже упоминавшаяся книга и статьи Мерклингера являются единственным разумным интернетным источником на тему глубины резкости при наклонах, однако это достаточно объемный и не слишком простой источник. Вообще, этот вопрос как-то не принято обсуждать, скажем и Steve Simmons и Jack Dykinga эту проблему обсуждают исключительно на пальцах, никаких разумных количественных данных в этих книгах нет (а другие мне не попадались).

Вместе с тем, умение фокусировать tilt-объектив "по шкале" или, хотя бы, ставить по шкале разумное начальное приближение - очень сильно экономит время, оставляя время на более творческую работу. Но помня о том, что у людей творческих большие таблицы выносят мозг, хочется разобрать один частный случай:

• Камера стоит вертикально (т.е. задняя стенка вертикальна).
• Плоскость резкости - горизонтальна или почти горизонтальна.

Наводка на "бесконечность"

Представим себе простейший случай: камера стоит на штативе на какой-то высоте, перед нами ровная горизонтальная поляна, мы хотим положить плоскость максимальной резкости строго на нее (т.е. на картинке 'Plane of sharp focus' совпадет с Marsh Grass).

Если наклонять (уклонять) объектив вниз, то плоскость резкости проходит на какой-то глубине J ниже объектива под каким-то углом Φ к плоскости "пленки" (сенсора). J зависит от фокусного расстояния объектива и его уклона, а Φ - еще и от дистанции фокусировки (при фокусировании на более ближний план, плоскость фокуса поднимается, см. анимированную картинку в начале).

В первых трех строчках нижеследующей таблицы показаны сочетания угла уклона 24-мм объектива и дистанции фокусировки, при которых плоскость резкости пройдет строго горизонтально на J метров ниже объектива (на строчки ниже третьей пока внимания не обращайте): Для 24-мм объектива табличка наводки на "бесконечность" такова:

24-mm Tilt-Shift: Focus distance and 900-Φ1 for horizontal focus (Φ) plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	1.38	0.69	0.46	0.34	0.28	0.23	0.20	0.17
Focus distance for Φ=900 (meters)	158	39	18	9.9	6.3	4.38	3.22	2.47
f/stop	900-Φ1 (grad) at f/stop
4	16	8.1	5.4	4.1	3.2	2.7	2.3	2.0
5.6	22	11	7.5	5.7	4.5	3.8	3.2	2.8
8	30	16	11	8.0	6.4	5.4	4.6	4.0
11	38	21	14	11	8.8	7.3	6.3	5.5
16	48	29	20	16	13	11	9.0	7.9
22	57	37	27	21	17	14	12	11

Расшифруем, например, для уклона объектива (тилта) 4⁰ первые три строчки таблицы:

• если мы повернем объектив вниз на 4⁰
• и поставим на шкале дистанций 9.9 метра
• то
  • плоскость максимальной резкости пройдет на 0.34 метра ниже камеры
  • и будет строго горизонтальной.

Перейдем теперь к следующим строчкам таблицы.

Помимо плоскости полной резкости (которую мы вывели горизонтально), есть еще ближняя (верхняя) и дальняя (нижняя) границы клина глубины резкости (между линиями 'Near Limit' и 'Far Limit' на рисунке). Раз границу полной резкости мы разместили горизонтально, то дальняя граница идет ниже горизонта и нам неинтересна, а ближняя - выше горизонта и нам надлежит понимать под каким углом, чтобы расположить нужные объекты в резкости.

В нижних строках таблицы показано, под каким углом к горизонту проходит эта плоскость (ближняя граница резкости) при заданном уклоне объектива и дистанции фокусировки и разных значениях диафрагмы. Картинка достаточно простая, но лучше ее артикулировать:

• Чем закрытее диафрагма, тем больше (шире) клин резкости, хотя с закрытием диафрагмы его расширение постепенно замедляется (за формулами обращайтесь в книгу Мерклингера, не хочу перегружать ими текст).
• С увеличением угла уклона объектива, клин резкости стремительно сужается.

Поле зрения 24-мм объектива - около 47⁰ по короткой стороне кадра 24x36, при вертикальном положении задней стенки камеры верхняя половина поля зрения составляет, соответственно, примерно 24⁰. Таким образом, при передней плоскости резкости проходящей под этим углом к горизонту или выше, резкими будут любые достаточно удаленные объекты. Как мы видим из таблицы, это возможно только для небольших углов уклона объектива, а с ростом уклона верхняя граница резкости стремительно приближается к горизонтали.

Достаточно удаленные объекты поминаются по той причине, что клин резкости начинаются не от объектива, а на J метров ниже, соответственно для близких объектов ситуация непопадания в резкость вполне возможна (совсем без формул не получается: верхняя граница поля резкости пересечет линию "оси камеры" на расстоянии J*tg(Φ₁), скажем для f/5.6 и уклона 1⁰ это будет 3.4 метра).

Таблица посчитана исходя из обычного для узкоформатных камер кружка нерезкости 0.03 миллиметра. Если вам люб, скажем, кружок в 0.015 мм, то прикройте диафрагму на два стопа, относительно показанного в таблице.

Наводка на "гиперфокус"

"Гиперфокус" взят в кавычки т.к. на самом деле имеется в виду схема распределения резкости, аналогичная изображенной на схеме выше: нижняя (дальняя) граница клина резкости проходит горизонтально ("по траве"), плоскость максимальной резкости и ближняя плоскость приемлемой резкости — выше горизонта, под каким-то углом.

Так как раскрытие клина зависит (при фиксированном уклоне) от диафрагмы, то оптимальная дистанция фокусировки, при которой нижняя граница клина горизонтальна, тоже зависит от нее, соответственно цифр в табличке больше.

В таблице ниже:

• D - дистанция фокусировки по шкале при заданном уклоне объектива и диафрагме, такая чтобы дальняя плоскость приемлемой резкости стала бы горизонтальной.
• Φ - угол между задней стенкой камеры и плоскостью максимальной резкости.
• Φ₁ - угол между задней стенкой камеры и ближней плоскостью приемлемой резкости.

Все прочие обозначения, да и общий принцип организации таблицы - такой же. Естественно, значения J при том же уклоне объектива - те же самые.

24-mm Tilt-Shift distance (D), 900-Φ, and 900-Φ1 for horizontal lower acceptable focus plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	1.38	0.69	0.46	0.34	0.28	0.23	0.20	0.17
	Distance scale, 900-Φ and 900-Φ1 angles (degree)
f/stop	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1
4	4.7 16 30	4.3 8.1 16	3.8 5.4 11	3.2 4.1 8.0	2.7 3.2 6.4	2.3 2.7 5.4	1.9 2.3 4.6	1.6 2.0 4.0
5.6	3.4 22 38	3.2 11 22	2.9 7.5 15	2.6 5.7 11	2.2 4.5 8.9	1.9 3.8 7.4	1.7 3.2 6.4	1.5 2.8 5.6
8	2.4 30 48	2.3 16 29	2.1 11 20	2.0 8.0 16	1.8 6.4 13	1.6 5.4 11	1.4 4.6 9.0	1.2 4.0 7.9
11	1.8 38 57	1.7 21 37	1.6 14 27	1.5 11 21	1.4 8.8 17	1.3 7.3 14	1.2 6.3 12	1.0 5.5 11
16	1.2 48 66	1.2 29 48	1.1 20 36	1.1 16 29	1.0 13 24	0.96 11 20	0.90 9.0 17	0.83 7.9 15
22	0.89 57 71	0.88 37 56	0.86 27 45	0.83 21 37	0.79 17 31	0.75 14 26	0.71 12 23	0.67 11 20

Как видим, мы выиграли практически вдвое для тех случаев, когда клин резкости был узким и несколько меньше в случаях, когда он был достаточно широким. "Все удаленные предметы - резкие" (в пределах заданного кружка нерезкости) возможно даже для уклона 5 градусов (при f/16), при этом верхняя граница клина резкости будет пересекать ось камеры на расстоянии 0.6 метра (т.к. величина J уменьшилась за счет наклона).

Другая оптика

Чтобы владельцам других T-S объективов для узкого формата не было обидно, привожу такие же таблички для двух самых распространенных фокусных расстояний.

45mm

Поле зрения этого объектива примерно вдвое меньше, около 28⁰ по короткой стороне, состояние "все что в поле зрения - резко" достижимо примерно при тех же углах уклона и значениях диафрагмы. Но J растет пропорционально фокусному расстоянию, ближнее поле резкости меняется соответственно.

45-mm f/2.8 Tilt-Shift: Focus distance and 900-Φ1 for horizontal focus (Φ) plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	2.58	1.29	0.86	0.65	0.52	0.43	0.37	0.32
Focus distance for Φ=900 (meters)	295	74	33	18	12	8.2	6.0	4.62
f/stop	900-Φ1 (grad) at f/stop
2.8	6.1	3.1	2.0	1.5	1.2	1.0	0.9	0.8
4	8.7	4.4	2.9	2.2	1.7	1.4	1.2	1.1
5.6	12	6.1	4.1	3.0	2.4	2.0	1.7	1.5
8	17	8.6	5.8	4.3	3.5	2.9	2.5	2.1
11	23	12	7.9	5.9	4.7	3.9	3.4	2.9
16	31	17	11	8.6	6.9	5.7	4.9	4.3
22	40	22	15	12	9.3	7.8	6.7	5.8

45-mm f/2.8 Tilt-Shift distance (D), 900-Φ, and 900-Φ1 for horizontal lower acceptable focus plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	2.58	1.29	0.86	0.65	0.52	0.43	0.37	0.32
	Distance scale, 900-Φ and 900-Φ1 angles (degree)
f/stop	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1
2.8	22 6.1 12	18 3.1 6.1	14 2.0 4.1	10 1.5 3.0	8.0 1.2 2.4	6.1 1.0 2.0	4.8 0.9 1.7	3.9 0.8 1.5
4	16 8.7 17	14 4.4 8.6	11 2.9 5.8	8.9 2.2 4.3	7.0 1.7 3.5	5.5 1.4 2.9	4.5 1.2 2.5	3.6 1.1 2.1
5.6	12 12 23	10 6.1 12	8.9 4.1 8.0	7.3 3.0 6.0	6.0 2.4 4.8	4.9 2.0 4.0	4.0 1.7 3.4	3.4 1.5 3.0
8	8.2 17 31	7.6 8.6 17	6.8 5.8 11	5.8 4.3 8.6	5.0 3.5 6.9	4.2 2.9 5.7	3.5 2.5 4.9	3.0 2.1 4.3
11	6.1 23 40	5.7 12 22	5.2 7.9 15	4.6 5.9 12	4.1 4.7 9.3	3.5 3.9 7.8	3.1 3.4 6.7	2.7 2.9 5.8
16	4.2 31 50	4.0 17 31	3.8 11 22	3.5 8.6 17	3.2 6.9 13	2.8 5.7 11	2.5 4.9 9.6	2.2 4.3 8.4
22	3.1 40 59	3.0 22 39	2.9 15 29	2.7 12 22	2.5 9.3 18	2.3 7.8 15	2.1 6.7 13	1.9 5.8 11

90mm

Поле зрения еще вдвое уже (15⁰ по короткой стороне кадра 24x36 и 22⁰ по длинной), J увеличивается еще вдвое, исходя из чего и следует рассматривать данную табличку.

90mm f/2.8 Tilt-Shift: Focus distance and 900-Φ1 for horizontal focus (Φ) plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	5.16	2.58	1.72	1.29	1.03	0.86	0.74	0.65
Focus distance for Φ=900 (meters)	591	148	66	37	24	16	12	9.2
f/stop	900-Φ1 (grad) at f/stop
2.8	3.1	1.5	1.0	0.8	0.6	0.5	0.4	0.4
4	4.4	2.2	1.5	1.1	0.9	0.7	0.6	0.5
5.6	6.1	3.1	2.0	1.5	1.2	1.0	0.9	0.8
8	8.7	4.4	2.9	2.2	1.7	1.4	1.2	1.1
11	12	6.0	4.0	3.0	2.4	2.0	1.7	1.5
16	17	8.6	5.8	4.3	3.5	2.9	2.5	2.1
22	23	12	7.9	5.9	4.7	3.9	3.4	2.9

90mm f/2.8 Tilt-Shift distance (D), 900-Φ, and 900-Φ1 for horizontal lower acceptable focus plane
Tilt angle:	10	20	30	40	50	60	70	80
J, meters	5.16	2.58	1.72	1.29	1.03	0.86	0.74	0.65
	Distance scale, 900-Φ and 900-Φ1 angles (degree)
f/stop	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1	D 900-&Phi 900-Φ1
2.8	83 3.1 6.1	58 1.5 3.1	39 1.0 2.0	27 0.8 1.5	19 0.6 1.2	14 0.5 1.0	11 0.4 0.9	8.5 0.4 0.8
4	61 4.4 8.7	46 2.2 4.4	33 1.5 2.9	24 1.1 2.2	18 0.9 1.7	13 0.7 1.4	10 0.6 1.2	8.2 0.5 1.1
5.6	45 6.1 12	36 3.1 6.1	28 2.0 4.1	21 1.5 3.0	16 1.2 2.4	12 1.0 2.0	9.7 0.9 1.7	7.8 0.8 1.5
8	32 8.7 17	28 4.4 8.6	22 2.9 5.8	18 2.2 4.3	14 1.7 3.5	11 1.4 2.9	8.9 1.2 2.5	7.3 1.1 2.1
11	24 12 23	21 6.0 12	18 4.0 7.9	15 3.0 5.9	12 2.4 4.7	9.9 2.0 3.9	8.1 1.7 3.4	6.8 1.5 2.9
16	16 17 31	15 8.6 17	14 5.8 11	12 4.3 8.6	9.9 3.5 6.9	8.4 2.9 5.7	7.1 2.5 4.9	6.0 2.1 4.3
22	12 23 40	11 12 22	10 7.9 15	9.3 5.9 12	8.2 4.7 9.3	7.1 3.9 7.8	6.2 3.4 6.7	5.3 2.9 5.8