О Нумерологии
Количество дискуссий "о статистике" в которых я тут, сдуру, участвую, начинает меня нервировать. Хочу записать основные тезисы, дабы потом просто давать ссылку, а не писать одно и то же десять раз.
Предуведомление
Для создания хоть какой-то конструктивной атмосферы в обсуждении, вынужден сообщить:
- Я никоим образом не пытаюсь оспорить наличие фальсификаций на прошедших выборах о чем просто утомился уже говорить. Есть участки, где просто йобаный стыд, есть зафиксированные расхождения между копией протокола у наблюдателя и сайтом ЦИК (и эти расхождения, как правило, за одну партию), есть всякие подозрительные случаи, когда наблюдателя выгнали, а на сайте ЦИК что-то абсолютно не похожее на результаты по соседним участкам.
- Вышесказанное не означает, что любая странность должна трактоваться против Чурова и ЕР.
- Вышесказанное не означает, что любая наукообразная аргументация от противников Чурова/ЕР должна восприниматься некритически.
- Ну и если мы про статистическую науку, так давайте действовать как-то наукообразно, а не кто кого громче заклеймит и перекричит.
О Гауссиане и Центральной Предельной Теореме
В качестве обоснования гауссианы в подавляющем большинстве дискуссий поминается "Центральная Предельная Теорема", исходя из которой эта гауссиана и обязана получаться.
Центральная Предельная Теорема в классическом выражении говорит нам (вот прямо по википедии):
- сумма бесконечной последовательности независимых случайных величин,
- одинаково распределенных т.е. имеющих одинаковое матожидание и дисперсию,
- будет распределена нормально (т.е. по гауссиане)
Но
- Откуда берется мысль, что избиратели по стране (или по Москве) голосуют одинаково т.е. с одинаковым мат-ожиданием и дисперсией? Насколько я знаю, результаты выборов по регионам - заметно (и значимо) отличаются. А значит никакой гауссианы по стране не получится.
- Откуда берется мысль о независимости? Насколько я знаю, явка на разных выборах - сильно отличается. А значит есть какие-то факторы, которые решение вопроса "не сходить ли на участок" значимо сдвигают.
- (Еще раз) откуда берется мысль о независимости, если, чудесным образом, сумма всех результатов (голоса за партии + незачтенные бюллютни) по каждому из участков равна строго 100%? Результаты за партии - линейно зависимы.
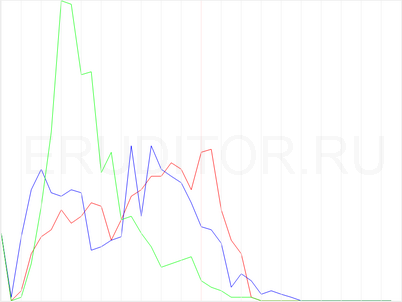
Отмечу, что если бы идея о гауссиане соблюдалась бы на практике, то всеобщие выборы были бы не нужны, было бы вполне достаточно нескольких сотен участков, причем вовсе не обязательно было бы их распределять по стране.
Update: украду еще пару графиков из статьи Статистический анализ результатов израильских выборов 2009 года
1. Распределение по партиям:

2. Распределение по партийным блокам

В-общем, тезис о том, что "во всех нормальных странах ВСЕГДА ГАУССИАНА" можно считать не просто недоказанным, а противоречащим практике.
Зависимость результата от явки
Утверждение: результат не должен зависеть от явки (ибо гауссиана и вообще не должен). И уж тем более, не может быть так, что только у одной партии он так зависел (с углом графика явка-голоса под 45%). Есть единственная модель - вброс за правящую партию.
Упрощенную модель явления я уже описывал, у меня нет никаких демографических обоснований этой модели, она просто не противоречит никаким физическим законам.
Обратимся к опыту развитой английской демократии (сопру еще один график у Кузнецова):
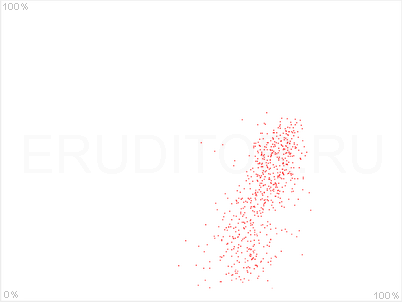
Получается, так бывает. Более того, похоже что каждый явившийся избиратель консерваторов вбрасывал минимум два бюллютня.
Подобная же картина наблюдается и в Израиле, см. статью по ссылке выше.
Гребенка Чурова
Все видели эту гребенку (пики на кратных процентах: 50, 60, 75 и так далее), что якобы является свидетельством накруток за ЕР.Многие, я надеюсь, читали и о другом объяснении, которое заключается в целочисленной арифметике: 50% голосов ровно дадут исходы 7 из 14, 8 из 16, 9 из 18 и так далее по всем размерам участков. И для участка с 8-ю явившимися избирателями возможны исходы с шагом 12.5% и никакие иные. А 51% ровно - получается куда меньшим числом способов. Аналогично 60% (3/5) будут возникать чаще, чем 59 или 61 (или 59.9 и 60.1 если взять бины помельче).
Понятно, что рассуждая таким образом нельзя отличить вброс (ровно на 50%, "ну давайте парочку добросим, а то у нас 49.9") от математических эффектов. Потому что и 50% и 60% - это круглые цифры, которые приятны не только целочисленной арифметике, но и избиркому.
По счастью, есть исключения: 2/3 (66.67%) и 7/8 (87.5%) - цифры не круглые, избиркомам неинтересные, то есть пики там будут именно за счет целочисленных эффектов.
Я, блин, не поленился, выкачал данные и построил график с бинами через 0.1% для голосов за ЕР. Вот кусочек его, от 48 до 82%. Бины проведены через 0.1% и "тупо" (т.е. номер бина - это int(процент*10), если рисовать менее тупо как int((процент+0.05)*10), то эффект сглаживается:

Как видим, пик на 2/3 имеется, причем он ровно на 2/3 (66.7), избиркомы тянули бы до 67%, как мне кажется. Пик на 65% тоже есть, но он меньше по величине, чем на 2/3.
Вывод: как минимум частично, пики на круглых дробях (1/2, 3/5, 2/3, 3/4, 4/5) объясняются целочисленной арифметикой. Пик на 7/8 (87.5%) совсем невыразительный (участков мало), но тоже имеется.
Update: Как нам подсказывают в комментариях, гребенка есть и для КПРФ на 20% (1/5) и на 25% (1/4) и для других партий - тоже. ПГ на том графике - просто случайная величина, так ведь тоже. Кругом враги!
Update2: продолжение про гребенку Чурова - в следующем посте. Как мне кажется, тема закрыта совсем, никаким "свидетельством фальсификаций" эта гребенка не является, это всего-лишь артефакт обработки данных.
Мораль
Мораль простая: не все "очевидные" особенности стат-данных по выборам есть результат злонамеренности. И гауссиана отсутствует в развитых демократических странах и странные пики - не обязательно странные. Тщательнее надо. Если статистика - то прямо вот от основ, независимость, случайность, вид распределения....
Comments
http://realcorwin.livejournal.com/275122.html#comments Вот т
http://realcorwin.livejournal.com/275122.html#comments
Вот тут наглядненько, как меняются пики при изменении квантования.
Я проверял собственную идею про 2/3, потому что это такое ме
Я проверял собственную идею про 2/3, потому что это такое место, до которого искусственно накручивать было бы странно (ровно до 66.7 для бина 0.1, а не 67)
Но как нам тут ниже подсказывают, на 1/5 и 1/4 пики есть и у "партии Гаусса"
Интереснее что есть небольшой пик у КПРФ на 50%. На Чурова э
Интереснее что есть небольшой пик у КПРФ на 50%. На Чурова это никак не спишешь.
почему это не спишешь
почему это не спишешь ???
Чтобы добавить ЕР надо убавить у остальных, если "испорченных" не хватит.
И вообще, если есть решимость доводить ЕР до "не менее Х", то весьма вероятна и решимость "не доводить врагов до более, чем Y"
Т.е. этот артефакт просто должен быть у всех сразу, только в разныъх частях графика. И по естественному и по конспирологическому объяснению
психи! только запутали...
психи! только запутали...
Ок. Доводы убедительны. Тогда скажите, пожалуйста, почему эт
Ок. Доводы убедительны. Тогда скажите, пожалуйста, почему эта гребенка и отсутствие гауссианы наблюдаются только для ЕР? Ведь с точки зрения статистики все партии равны. Или кто-то, получается, равнее даже по математике? Ну допустим гаусиана там получилась, тут нет... Ладно. НО гребенка то все-равно должна быть, исходя из ваших тоже расчетов.
<i>Тогда скажите, пожалуйста, почему эта гребенка и отсутств
Это не так.
ПГ - тут вообще случайная величина. Гребенка для нее, как несложно заметить, наблюдается.
Комментарий хозяина блога:
Комментарий хозяина блога: катинка выше уменьшена, чтобы не рвать верстку. Для просмотра в полный размер - View Image по правой кнопке мыша.
В смысле, на 1/8 или там 1/6? Я туда просто не смотрел. Я и
В смысле, на 1/8 или там 1/6?
Я туда просто не смотрел. Я и этот то график заставлял себя построить дня три.
а какое количество малых участков? (скажем не более 300 изби
а какое количество малых участков? (скажем не более 300 избирателей)
мне кажется такие участки обеспечивают от силы 1-2 процента от общего числа избирателей.
думается, что если выкинуть данные по этим участкам, то пики, вызванные целочисленной арифметикой, должны существенно сгладиться, при этом картина распределения по партиям не должна пострадать.
Их ~21 тысяча (зарегистрированных избирателей < 300) Разбир
Их ~21 тысяча (зарегистрированных избирателей < 300)
Разбираться с ними отдельно/без них - смысла не имеет. Графики, которые "все доказывают" - они же по всем участкам построены.
то есть сильно меньше миллиона избирателей, на результат не
то есть сильно меньше миллиона избирателей, на результат не влияет.
зато если без них не будет всплесков - значит версия опровергнута, можно считать, что всплески продукт небольших избирательных участков (где они хорошо объясняются изложенной версией).
а если часть неоднородностей всё равно сохранится - повод задуматься ещё раз.
PS: будь я злонамеренным членом избирательной комиссии - ни за что бы не получилось у меня на выходе 50% или подобных "красивых цифр".
упс, с порядком ошибся - несколько миллионов <i>потенциальны
упс, с порядком ошибся - несколько миллионов потенциальных избирателей, всё равно роли не сыграют такие участки в результате.
а вот всплески вполне могут дать.
Да, наверное часть всплесков - от таких вот мелких. Я не в
Да, наверное часть всплесков - от таких вот мелких.
Я не вижу особого смысла играться с данными таким образом т.к. обсуждаем то мы "классическую гребенку Чурова", прогремевшую на всю страну, а не то, как выборные данные представлять правильно.
Правильно - можно бин пошире, правильно расположенный (не 50-50.5 а 49.75-50.25) ну и погладить скользящим окном.
Один блоггер просто вырезал
Один блоггер просто вырезал все пики плюс минус 0,5%. Обще количество голосов за ЕР уменьшилось на полпроцента, что-ли. Тогда он взял и отрезал все участки, где голосов за ЕР было 75% и более - сильный ход. Финальный результат уменьишлся всего на 7%...
Ну в Москве (графики для
Ну в Москве (графики для который выглядят странно) до 75 не везде и тянули. И 7% - это много, это мест 30 в Думе.
Давайте с основ. Множество элементарных событий = {w1 - изб
Давайте с основ.
Множество элементарных событий = {w1 - избератель выбрал 1 пункт в бюллетене, w2 - избератель выбрал 2 пункт в бюллетене, итд}
Дальше смотрим что такое случайная величина - это функция из множества элементарных событий в множество вещественных чисел, отвечающая некоторым условиям.
Вы пишите:
В случае выборов, под "независимой случайной величиной" имеет смысл понимать результат голосования одного избирателя.
Тогда у вас выйдет просто на каждого изберателя будет по какому то числу.
Более того, так как один избератель голосует один раз, то говорить о его дисперсии или мат. ожидании нельзя, т.к. эти характеристики появляются только у множества измерений.
В тех же исследованиях, которые вы опревергаете, дело обстоит чуть иначе.
Там исследуется случайная величина - число проголосовавших за конкретную партию на конкретном участке.
Т.е. берутся данные по одному участку, определяется событие A1 = {w1}. Далее для простоты введем индикаторную величину Ik = 1, если при kтом опыте событие A1 произошло, Ik = 0, если не произошло.
Далее берем случайную величину F = сумме Ik.
И вот когда мы возмем множество таких случайных величин, по всем участкам для события A у нас и будет искомое множество.
Поправка, в последнем абзаце следует читать: ...для события
Поправка, в последнем абзаце следует читать:
...для события A1 у нас и будет искомое множество.
Естественно, одно событие не имеет распределения, оно одно и
Естественно, одно событие не имеет распределения, оно одно и оно уже случилось.
А вот множество событий - имеет.
Ну вот кидаем монету, каждое бросание имеет какой-то исход. Единственный. А 100 бросаний - уже и мат-ожидание и дисперсию.
Вон тут хвостатые израильские графики в коллекцию: http://me
Вон тут хвостатые израильские графики в коллекцию:
http://meast-ru.livejournal.com/1765703.html
Ага, спасибо. Попрал чужие авторские слова и добавил картино
Ага, спасибо. Попрал чужие авторские права и добавил картинок к тексту.
А Вас не смущает тот факт,
А Вас не смущает тот факт, что графики не _почти совсем не гауссианы_, как в той же Великобритании, а _почти гауссианы_, за фактом низких процентов для всех партий, кроме ЕР, и высоких для ЕР?
Я обсуждаю очень узкий мем
Я обсуждаю очень узкий мем "Тут не гауссиана, а должна быть гауссиана, во всех приличных странах - гауссиана, это всегда так, вообще всегда" (лучший образец я видел у lleo).
На вопрос "а почему" - начинают рассказ о центральной предельной теореме.
Так вот: "в приличных странах" - необязательно гауссиана. Может быть с двумя максимумами (с тремя, если 0 считать) как в Англии, а может быть вообще мутант как в Израиле.
Точка.
И после закрытия этой темы ("обязана быть гауссиана") можно заниматься дальше нормальной наукой - какое же все-таки распределение и почему. И откуда в Израиле мутанты.
А почему бы не пойти от
А почему бы не пойти от противного? Давайте посчитаем, что гауссовское распределение - это норма при свободном и независимом волеизъявлении граждан, а имеющиеся исключения в виде GB/IL - это именно исключения, причем, возможно, являющиеся признаком имеющихся в этих странах проблем в выборной/политической системах (не таких серьезных, как в России, но ведь и масштаб перекосов другой)?
Чтобы получить гауссиану на
Чтобы получить гауссиану на выходе (сумма по регионам и т.п.) на входе должны быть распределения с одинаковым матожиданием/дисперсией. Т.е. все регионы - одинаковы.
На практике, как мы знаем, какие-то штаты голосуют всегда за демократов, какие-то - за республиканцев, какие-то - как пойдет.
Кроме того, известен термин Джерримендеринг - такая нарезка округов, которая дает преимущество одной из партий. То есть территориальные группы избирателей таки значимо отличаются по предпочтениям и матожидание/среднее по разным территориям - разные, т.е. сумма гауссианой в общем случае не будет.
Британский график на
Британский график на гауссиану ну никак не похож. Есть подобный по Польше - та же картина. Кто-то даже по критериям их прогнал - не сходится. Наш график за ЕР очень похож на британские и польские, только высота пониже.
Есть мнение, что это особенность всех выборов в неоднородных обществах с выраженной лидирующей позицией одной из партий: графики всех отстающих будут напоминать Гауссиану (но не являться ей), а лидирующей - что-то вроде логнормального графика.
Ну да, один знакомый
Ну да, один знакомый бизнесмен так и сказал - это же типичная картина для лидера рынка, он расширяется и занимает все пространство, а конкуренты копошатся в нишах.
> Как видим, пик на 2/3 имеется, причем он ровно на 2/3 (66.
> Как видим, пик на 2/3 имеется, причем он ровно на 2/3 (66.7), избиркомы тянули бы до 67%, как мне кажется.
Этот пик тоже объясним приписками. Разумеется никто не рассуждал так: "А давайте напишем за ЕР 66 и 6 в периоде процентов, потому что на число зверя похоже". Но могли рассуждать так: "- Сколько за сегодня проголосовало? - Ну-у-у... человек двести двадцать. - Пиши триста! - А сколько проголосовало правильно? - Пиши двести"!" Вот вам и пик на 66.6(6) исключительно из любви к круглым числам.
Легенда про "гребенку Чурова" - это то, что "тянули до кругл
Легенда про "гребенку Чурова" - это то, что "тянули до круглого числа", что для ЕР, очевидно, в существенной степени не так (пик на 2/3 сильно выше чем на 65%, например) Кроме того, на графике КПРФ мы видим пики на 1/4 и 1/5 и что-то я сомневаюсь, что их туда затянули. Не говоря про Партию Гаусса, которая чистый симулятор, а имеет пик на 50% примерно как у ЕР (если в относительных долях)
То есть наличие гребенки не является подтверждением приписок. И, естественно, не может являться их опровержением.
>Кроме того, на графике КПРФ
>Кроме того, на графике КПРФ мы видим пики на 1/4 и 1/5 и что-то я сомневаюсь, что их туда
>затянули
Их могли туда не "затягивать", а, напротив, опускать
Да вы посмотрите на график
Да вы посмотрите на график (он тут выше в каментах) - пик вверх и пик вниз, рядом.
Нет никакого смысла затягивать/опускать на 0.1%, чистый численный артефакт.
И такие же пики - на полностью симулированной (генератором случайных чисел) "Партии Гаусса"
Взгляните на сегодняшнюю версию статьи Кузнецова. Автор спеш
Взгляните на сегодняшнюю версию статьи Кузнецова. Автор спешно переделывает математическую составляющую текста. Что, правда, никоим образом не отражается на оскорбительных характеристиках "оппозиционных математиков", с выводами которых он на текущий момент уже согласен.
Взгляните на сегодняшнюю версию статьи Кузнецова. Автор спеш
Взгляните на сегодняшнюю версию статьи Кузнецова. Автор спешно переделывает математическую составляющую текста. Что, правда, никоим образом не отражается на оскорбительных характеристиках "оппозиционных математиков", с выводами которых он на текущий момент уже согласен.
Мне от Кузнецова нужны только графики по UK. Которые - не ме
Мне от Кузнецова нужны только графики по UK. Которые - не меняются. Ну и кроме них уже есть графики по Израилю.
Израильский график с хвостом
Израильский график с хвостом 100% или около того голосовавших на отдельных участках только подтверждает версию вброса. Это ултрарелигиозные люди. Они голосуют за того, за кого скажет рав - бесспорный авторитет для общины. Там нет людей с другим мнением. Но для Израиля это имеет вполне понятное и явное объяснение. А вот для России сложно предположить места компактного проживания поклонников одной единственной партии. Не настолько, чтобы это хоть как-то заметно появилось на графике.
1. А почему в ауле на Кавказе
1. А почему в ауле на Кавказе не может быть авторитета?
2. Тува: Чадан, понятно, дал 100% за Шойгу (там даже улица Шойгу есть, при живом Герое), остальная тувинская тува - тоже недалеко от этого. Там просто культ.
Слушай, возьми результаты по
Слушай, возьми результаты по Москве и другим миллионникам и не трынди по аулы. Либо не бери аулы. Нашел исключения с религиозными евреями и рад. У нас такого не будет, хоть патриарх и говорит,что верит в Путина.
Вас уже поправили с неграмотным знанием и использованием мат. аппаратом,закрыли бы свой пост уже.
Выдумки про круглые цифры, это лишь акцентирование частного случая прикормленными блоггерами того факта, что председатели комиссий для подгона под приемлимые проценты брали круглое число бюллетеней , чтобы считать было проще.
И что за бред для домохозяек про простоту совпадения на участках количества голосовавших за ЕР и остальных, чтобы получить 50 процентов?!
Вас уже поправили с
Слушай, возьми результаты по Москве и другим миллионникам и не трынди по аулы.
Ну да, логично, настоящие люди живут только в Москве и миллионниках. Остальные 3/4 населения страны - гарантированно являются быдлом, их мнение нормальным людям неинтересно.
Вас уже поправили с неграмотным знанием и использованием мат. аппаратом
Это где же?
Это ты их такими считаешь,
Это ты их такими считаешь, как оказывается, ведь мы говорили про аулы и
Израиль. Я так к тому, что Москва и миллионики более свободные, и если ты действительно хочешь поверить честно ЦИК, то надо брать их.
Тот математик, что указал на твои ошибки, вовсю писал "избЕратели" - легко найти в поиске.
С другими опровержениями, значит, согласен. Исправь статью тогда
Ну подождите, плакаты с
Ну подождите, плакаты с "гребенкой чурова" - рисовали по всем участкам? Ну и я рисую.
"Математиков", пишущий "избератели" было двое, один писал ерунду, а со вторым мы и не спорили.
Я тоже заметил, что не
Я тоже заметил, что не спорили, а теоретическую часть не поправили.
Вообще все замечания, с которыми не поспоришь, учтены в статье не бы
Не хочется, чтобы бывало всё по-честному, не приводите в пример страны в которых выборы по своим законам.
Или честно покажите гребёнку, которая действительно показывает были или нет фальсификации - можно ли использовать Гаусса.
Про "можно ли использовать
Про "можно ли использовать Гаусса" - в тексте все написано.
Остальную часть вашего комментария я понимаю с трудом. Не волнуйтесь, пишите спокойнее, перечитывайте написаное перед публикацией.
С телефона этот блог не фига
С телефона этот блог не фига не даёт нормально читать и писать.
Про Гаусса - если вы обвиняете маленькие участки в аульности, то проверьте большие города, чтоб не говорить, что у нас как в Израиле.
И я ещё раз говорю, что ваша теоретическая часть безграмотна, равно как и объяснение, что красивые проценты вероятны больше чем не красивые!
И я ещё раз говорю, что ваша
И я ещё раз говорю, что ваша теоретическая часть безграмотна
Отлично. Давайте ее обсудим. У вас есть какая-то нестандартная формулировка Центральной Предельной Теоремы?
Ммм, как вам надо пальцем,
Ммм, как вам надо пальцем, тыкать, что и как, оказывается.
Ещё раз найдите с "избЕратилями", почитайте, что за случайная величина должна быть - количество проголосовавших за такую-то партию - и уберите из своего текста бред, про отсутствие независимости этого числа.
Казалось бы, если мы выражаем
Казалось бы, если мы выражаем набранные голоса в процентах, то зависимость никуда не денется.
Казалось бы... Даже не знаю,
Казалось бы...
Даже не знаю, почему этот блог должен что-то доказывать, если:
1) автор не знает, какую надо выбрать случайную величину, и выбирает что-то непонятное, а график строит "как у всех", которые случайную величину берут вполне адекватную. Теория одна, графики другие.
2) автор даже не понимает, в чём состоит независимость случайных величин.
3) при этом выдуманная домохозяйская зависимость занимает целых два пункта и одно из центральных мест в невозможности использовать гауссиану
Если график у меня - "как у
Если график у меня - "как у всех" и этот график негодный, то революционные графики на плакатах - тоже негодные?
Ещё раз перечитайте товарища
Ещё раз перечитайте товарища с "избЕрателями".
У тех всех график соответствует их теории. А у вас теория своя, пропутинская, он бы так же не соображая в матстате про случайные величины изъяснялся, а графики строятся по их теории, исходя из их случайных величин.
Так ведь по осям одно и то же
Так ведь по осям одно и то же и данные те же.
Прекрасно, тогда причём тут
Прекрасно, тогда причём тут ваша доморощенная теория?
Сотрите всё :-) особенно про отсутствие независимости у случайных величин.
Если хотите использовать графики, которые строят все на совершенно других протоколах
Как связаны графики и теория?
Как связаны графики и теория?
У вас никак и это
У вас никак и это отстой
Теория - полная лажа
Но при этом вы пытаетесь что-то ею доказать
Данные же - объективны,
Данные же - объективны, существуют независимо от наличия теории?
Если их обрабатывать с
Если их обрабатывать с помощью кривой теории, а потом не менее криво комментировать, то получается хрен знает что.
Скажите прямо - почему не уберёте лажовую теорию? Не заплатили что ли. Или за ту заплатили на год вперед? :-D
Так вы против чего согласны
Так вы против чего согласны то?
Да, вы комментируйте, комментируйте. Мне за комментарии читателей - отдельно платят.
Здорово, хорошо
Здорово, хорошо устроились.
Надеюсь, за вынужденные повторы неудобных вам вопрос ов тоже вознаградят
" почему не уберёте лажовую теорию?"
Так ведь она настоящая, как
Так ведь она настоящая, как Колмогоров завещал. Ибо
- кто сказал, что по всей стране голосуют одинаково? Даже если взять данные только с участков где наблюдатели подписались что все хорошо - среднее разное.
- кто сказал, что дисперсия - одинаковая? Дисперсию вообще никто не изучал
- ну и на графике число комиссий - % голосов - будет не ЦПТ, а банальная сумма.
На сем дискуссию без аргументов, а только с эпитетами ("негодная") заканчиваю. Хотите обсуждать по сути - давайте содержательные аргументы.
"Исключения" - не только у
"Исключения" - не только у "религиозных евреев" (кстати, миф - религиозна отнюдь не бОльшая часть страны, плюс там ещё 20% арабов живёт), но и у, как минимум, Великобритании и Польши. Как говорят математики - отклонения от предполагаемой "апологетами Гаусса" картины должны быть во всех странах, где есть выраженная полярность мнений.
Миф, не миф, но участки, где
Миф, не миф, но участки, где эти религиозные составляют под сто процентов там достаточно. А у нас в обычных городах такого не было и быть не может. Ща отдыхаю на северном Кавказе, даже здесь, с кем не общался, кто за ЕР и за Путина голосовал не знают
Представил себе хипстера в
Представил себе хипстера в ауле, проводящего опрос "за кого вы голосовали".
Уважаемый, по данным, подтвержденным независимыми наблюдателями на думских выборах в Москве разброс за ЕР был более чем вдвое (плюс всякие выдающиеся участки, на которых очевидно были фальсификации).
На президентских выборах, под пристальным наблюдением, в той же Москве - разброс был еще феноменальнее (от общежития ВШЭ до Нагатино). Признаем теперь Нагатино несуществующим?
Зачем это было представлять
Зачем это было представлять и, тем более, писать, и я уж точно не в ауле и специально никого не спрашивал. Сами жалуются, что кругом ничего не меняется и выборы бесполезны в плане возможности влиять на власть, и в следующий раз они на выборы не будут тратить время.
А остальное зачем вами было написано? Понятное дело, на московских участках вряд ли живут негры из гетто, которые поголовно голосовали за Обаму. А путинский Питер тоже не был замечен в любви к его партии и лично к нему. Так что и делайте гауссиану по Москве, посмотрите,что получится :-)
У вас какие-то альтернативные
У вас какие-то альтернативные когнитивные способности.
Я пишу, что гауссианы а) не бывает б) и не должно быть (и в) - в этих координатах получится просто сумма гистограмм), а вы предлагаете мне ее делать?
А я вам написал, что ваши
А я вам написал, что ваши теоретические выкладки кроме цитат из Википедии имеют мало общего с теорией вероятности. Но исправлять не спешите.
Оттого и гауссиана.
Так где гауссиана то?
Так где гауссиана то?
Где-где, в теории есть, а на
Где-где, в теории есть, а на графиках отсутствует.
Что и требуется доказать, графики из-за волшебника Чурова получились сказочными, и ваше оправдание красивых процентов, что они более вероятны, тоже обман читателей. А оправдание аулами я предложил избежать постройкой графиков по крупным городам. Может, там будет всё нормально, но ай зассали :-D
Вот ведь какой Чуров
Вот ведь какой Чуров волшебник, пробрался и в Англию и в Польшу и в Израиль и в Штаты.....
" Как заявил Владимир Чуров
" Как заявил Владимир Чуров средствам массовой деградации: Никаких беспорядков против Путина в Москве не было. Работала шайка гипнотизеров и чревовещателей ."
Ой-йой-йой, опять этот довод, у нас в России полно гетто, где негры голосуют, или республиканские штаты есть, королева правит, и мы ребе слушаем, а власть у нас 12 лет ге менялась, цены на нефть упали, все в едином порыве решили её поменять, отсюда и цифры странные.
И вот что интересно, текст не меняется :-D хотите продолжать людям голову дурить
Вы от Краснодара отъедьте на
Вы от Краснодара отъедьте на юг, в Адыгею и оглядитесь.
И продолжайте комментировать, мне за вас премия будет.
А я на юге. Кругом джигиты -
А я на юге. Кругом джигиты - кабардинцы, черкессы, греки :-)
Не хрен кивать на аулы, не смешно уже.
Вы вообще понимаете, что за
Вы вообще понимаете, что за чушь несёте? :-)
Аргументы, что ваши графики не соответствуют вашим рассуждениям вначале, которые надо убрать, чтобы не путать людей.
Тем более, что по ссылке можно найти определение, отличающееся от вашего:
" сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному."
О, да тут и про сумму, и про не независимые, а слабо зависимые зачем же вы такой господин соврамши? Тем более, чтобы вы знали, тут и вообще в Тервере зависимость случайных величин означает зависимость друг от друга.
То есть если на 212 участке проголосуют 22 процента за ЕР, а не 23,то на соседнем 213 всё равно останется 34процента, если, конечно, ТИК не решит, что это мало :-)
Идите, учите формулировку
Идите, учите формулировку ЦПТ. Вместо википедии - возьмите учебник для ЦПШ хотя-бы.
Вторым шагом задумайтесь, что за сумма отображена на гистограмме голоса-количество избирательных комиссий
Чего-чего? Это ваша ссылка и
Чего-чего?
Это ваша ссылка и ваши рассуждения именно о ЦПТ!
Так вы прочтите ссылку дальше
Так вы прочтите ссылку дальше первого предложения. Ну, для начала.
Потом найдите учебник для ЦПШ, его тоже почитайте.
А потом расскажите: а какую такую вы сумму случайных величин углядели на гистограмме?
Вот ваши писульки: "
Вот ваши писульки:
" Центральная Предельная Теорема в классическом выражении говорит нам (вот прямо по википедии):
сумма бесконечной последовательности независимых случайных величин, одинаково распределенных т.е. имеющих одинаковое матожидание и дисперсию, будет распределена нормально (т.е. по гауссиане)"
Вы вообще сами читали. Там даже написано: "по Пидевикии".
Или вы в глаза долбитесь? И сразу вас можно поймать на вранье - в Пидевикии нет в определении ЦПТ "независимых", никаких матожиданий и дисперсий, которыми вы хотите запутать неподготовленного читателя. Вы просто лжёте и не можете считаться никаким источником и доказательством отсутствия гауссианы,если бы выборы не были сфальсифицированны.
А сумма случайных событий в виде того, что просуммированы все участки, где партия набрала столько-то процентов у вас на графиках, а не в теории.
Вы дальше первого абзаца
1)Вы дальше первого абзаца википедию прочитать не способны? Это, в принципе, нормально, ничего позорного в этом нет, просто удивительно для якобы научной дискуссии.
2)Суммой каких событий является счетчик участков (с таким-то процентом голосов)?
Мобильная версия Википедии -
Мобильная версия Википедии - я же на отдыхе, на Кавказ, который,оказывается не выбирает поголовно Путина и не радуется,что его кормят - показывает мне всего один абзац по вашей ссылке, и его вполне хватает.
С чем вы из процитированного в нём несогласны, научный вы наш, что так и не хотите исправлять свой самопальный текст?
Про независимость случайных величин вам стало понятно? Уберёте два абзаца своего ненаучного бреда - пункты 2 и 3?
Возьмите немобильную версию и
Возьмите немобильную версию и прочтите следующий абзац.
Наверное, я это сделаю после
Наверное, я это сделаю после того, как вы ответите на вопросы. Желательно честно.
Так в чем вопрос то?
Так в чем вопрос то? Сформулируйте, пожалуйста, самостоятельно, без отсылок неизвестно куда
Ещё раз повторю: С чем вы из
Ещё раз повторю:
С чем вы из процитированного мной из Вики (кстати,нарыл учебник определение крайне точное) несогласны, научный вы наш, что так и не хотите исправлять свой самопальный текст?
Про независимость случайных величин вам стало понятно? Уберёте два абзаца своего ненаучного бреда - пункты 2 и 3?
Я полностью согласен с
Я полностью согласен с определением из вики.
Которое про
...бесконечная последовательность независимых одинаково распределённых случайных величин
Да, ладно. Выделите ещё и
Да, ладно. Выделите ещё и бесконечная, чтобы определение, выбранное вами, стало ещё голимее. Вам вопросы по несколько раз надо писать, вот это определение из Вики чем вас не устраивает - может доказать его неправоту можете:
" сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному"
И ответьте уже на второй вопрос! Хватит уходить от ответа
Помимо независимости и
Помимо независимости и одинаковой распределенности существует еще такая мелкая проблема, что на гистограммах (в митинговых координатах) - не сумма случайных величин, а сложенные гистограммы.
Ожидать в этом месте работы ЦПТ было бы и вовсе странно - о чем я и пишу.
1) вы написали, что
1) вы написали, что определение неправильное - ответьте в чём?
2) во 2 и 3 пункте ненаучный бред, не имеющий никакого отношения к независимости случайных величин. Вы когда уберёте его? Он только пудрит мозг остальным.
Две случайные величины являются независимыми в случае участков, если 23 процента на участке с КОИБом у ЕР не повлияет на то, что на обычном участке процент у ЕР не поднимется до 59. А вы что за ахинею пишите?
То есть вы считаете
То есть вы считаете независимыми-случайными - результаты по отдельным участкам.
Ну, отлично.
Скажите, а где на гистограмме их сумма? Ну то есть если на одном участке 23, на другом - 59, то сумма должна быть 82, верно?
1) так ответ и не получен.
1) так ответ и не получен. Ай-яй-яй. Вообще "Предел" состоит в том,что последовательность случайных событий при их достаточно большом числе подчиняется нормальному закону распределения.
2) естественно, при честных выборах процент будет случайным - или 23 или 24 процента у ЕР - и, конечно, уменьшение процента на одном участке не должно повышать процент на другом
1) Далеко не всякие случайные
1) Далеко не всякие случайные события распределены по нормальному закону, даже в природе (рассмотрите скорости молекул в газе, число фотонов в световом потоке).
2) То что результаты наичестнейших выборов распределены не по этому закону - очевидно т.к. нормальное распределение имеет бесконечные хвосты (и в минус и в плюс), а результаты выборов оных хвостов не имеет. Кроме того, гауссиана - симметрична, ожидать такой симметрии для малых партий - невозможно (должен быть большой отрицательный хвост, но он не может возникнуть по самой процедуре).
Следовательно - гауссиана в чистом виде к выборам вовсе неприменима.
3) Для применения ЦПТ к выборам надо доказывать независимость, одинаковость мат-ожидания, одинаковость дисперсии. Ну и определить, что же именно мы складываем, для получения "суммы случайных величин"
4) В тех координатах, в которых строились послевыборные плакаты - о сумме вообще речь не идет, там суммируются гистограммы. Если есть два горба (село и город) - они не сложатся, а останутся двумя горбами.
Так и хочется сказать:
Так и хочется сказать: "мальчик, вы дурак? "
Я задал всего два вопроса.
Где хоть ответ на один?
1) что не так в определении ?
2) я уже объяснил вам, что в теории вероятности подразумевается под независимостью случайных величин! Когда вы сотрёте пункт 2 и 3 своих рассуждений ? И почему вы затягиваете с этим?
По-моему, вы зря стараетесь -
По-моему, вы зря стараетесь - править исходный пост я не собираюсь. Ответ на ваш вопрос "когда" - "никогда".
Возвращаясь же к ЦПТ: вы так и не объяснили, сумму чего (каких случайных величин) мы рассматриваем.
Вот у меня те же сомнения
Вот у меня те же сомнения возникли, что и у предыдущий ораторов.
Странная у тебя случайная величина берётся.
Попроси папу проверить свои выкладки. :-)
Тут какие-то бешеные сотни
Тут какие-то бешеные сотни комментариев, а предыдущие ораторы - разное говорят.
Вы против чего согласны то?
согласен с тем, что случайная
согласен с тем, что случайная величина странная берётся.
не такая, как в нашумевших исследованиях.
У меня берется? Это не я
у тебя, у тебя: В случае
у тебя, у тебя:
в оригинале рассматривалась другая случайная величина.
Вы договаривайте. "другая" -
Вы договаривайте. "другая" - какая?
ну, ты бы посмотрел оригинал
ну, ты бы посмотрел оригинал штоле. =)
случайная величина там "процент проголосовавших за определённую партию", соответственно, там несколько случайных величин (по количеству партий).
Если мы все еще обсуждаем
Если мы все еще обсуждаем центральную предельную теорему (которая говорит о сумме независимых случайных величин), то есть одна закавыка: сумма "процентов проголосовавших за определенную партию" равна единице (100%). Всегда (с партией "испортил бланк", естественно).
Что какбэ намекает нам на отсутствие независимости. И, следовательно, на неприменимость ЦПТ к этим какбэ случайным величинам.
тебе же написал rumata_vz:
тебе же написал rumata_vz: случайная величина -- индикатор события "за партию А проголосовало x% от голосовавших на участке".
теперь фиксируем одну партию А. и суммируем все эти индикаторы. откуда 100%-то?
(сорри, забыл про дискуссию, случайно сейчас вкладку открыл)
Если мы суммируем все эти
Если мы суммируем все эти индикаторы (% за партию) по участкам, то мы получим просто результаты выборов. Одно число. Ну то есть при нормальных выборах это число еще взвешивают на размер участка, но во всяких экспериментальных целях можно этого не делать.
А распределение (к коему, потенциально, применима ЦПТ) возникнет в результате нескольких (многих) выборов.
как это ты просуммировал N
как это ты просуммировал N функций и получил число? 8-O
Да, вы правы, я поленился
Да, вы правы, я поленился найти тот комментарий и интерпретировал то, что написали вы. Отмотал, прочитал.
Поясните пожалуйста две вещи
а) Распределение чего именно предлагается изучать? Числа участков где "ровно 500 голосов за партию А" (т.е. где "индикаторная функция" "ровно 500 голосов" дала 1)? Это, какбэ, требует повторных выборов
Или суммы всех индикаторных функций? Эта сумма, очевидно, равна количеству участков, т.е. независимости опять нет.
б) Какое отношение эти индикаторные функции имеют к графикам, которые таскали на митинги? На тех графиках по оси Х был "процент голосов за партию", по оси У - число участков с таким процентом (и крупная надпись про Гаусса и Чурова).
Я это, вроде, уже писал, но
Я это, вроде, уже писал, но напишу ещё раз, более подробно.
Берётся индикаторная функция такого события: за партию A проголосовало x% от избирателей пришедших на участок B.
Обозначаем эту функцию так: I_A(B,x). Это случайная величина, которую мы изучаем.
Далее рассматривается сумма по всем участкам: S_A(x) = I_A(B,x).
A фиксируем, рисуем графики, с ними выходим на митинг.
Этими словесными кружевами вы
Этими словесными кружевами вы маскируете обычную гистограмму.
А ошибка в этом рассуждении в том, что вы изучаете распределение не одной функции, а многих (такого количества, сколько нарисовали процентилей).
А у разных функций - разные матожидания и дисперсии, вы же не предполагаете их одинаковыми (т.е. при большом количестве испытаний 5% за партию А будет в примерно том же количестве участков, что и 85% за партию А)?
А раз они разные - ну так и исследуйте их отдельно, а не смешивайте в кучу.
многих функций -- это каких?
многих функций -- это каких?
Ну вот тех самых, I_A(1),
Ну вот тех самых, I_A(1), I_A(2) (название функции - по той процентили, которую она ловит).
I_A(B, x) -- это функция от x
I_A(B, x) -- это функция от x при фиксированных A и B.
Процентили тут ни при чём.
Она "принимает значение 1,
Она "принимает значение 1, если на участке B партия А набрала x процентов", правильно?
То есть "при фиксированных А и B" - у нее ровно одно значение, или 0 или 1?
ладно, забьём на индикаторные
ладно, забьём на индикаторные функции, вернёмся к случайной величине (я там повыше напишу)
итак, случайная величина --
итак, случайная величина -- процент проголосовавших на участке за определённую партию.
например, процент проголосовавших на участке за ЕдРо.
откуда тут берётся сто процентов?
Сумма этих случайных величин
Сумма этих случайных величин ("за едро", "за яблоко", "украл бумажку") - равна 100% в каждом из участков.
Следствие: эти случайные величины не являются независимыми.
лол, а кто предлагает
лол, а кто предлагает складывать проценты за разные партии??
Я предлагаю. Именно с целью
Я предлагаю. Именно с целью проверки гипотезы о независимости. Каковая гипотеза - не подтверждается.
независимости чего?
независимости чего?
Случайной величины.
Случайной величины.
Классическая ЦПТ сформулирована для "суммы независимых, одинаково распределенных случайных величин". Все слова важны.
а кто-то утверждает, что
а кто-то утверждает, что случайные величины "за едро" и "за яблоко" независимы?
Косвенно - призывая ЦПТ в
Косвенно - призывая ЦПТ в обоснование гауссианы.
нет. независимых величин
нет. независимых величин должно быть много, партий мало....
никто не призывает их складывать, и вообще их по отдельности рассматривают.
так что никто их независимость не предполагает....
я уж молчу про то что у них матожидание, разное, это всем понятно.
Отлично. Откуда мы тогда
Отлично.
Откуда мы тогда предполагаем гауссиану (и где, на каких графиках)?
А если мы продолжаем
А если продолжать настаивать на использовании ЦПТ (и Гаусса), то
даже наплевав на линейную зависимость, нужно откуда-то взять "сумму независимых случайных величин" (для классической ЦПТ - еще и с одинаковым матожиданием и дисперсией).
Сумма "процентов проголосовавших за едро" по всем участкам - это одна сумма за одни выборы.
С тем, что если в нескольких выборах удастся соблюсти условия про "одинаковое матожидание и дисперсию", то и результат будет распределен нормально - я и не спорю. Только это утверждение имеет нулевую ценность, выборы для того и делаются, чтобы оценить изменение матожидания.
да, ты прав, сумма
да, ты прав, сумма действительно одна получится.
ну ок, я ещё подумаю над обоснованием на досуге, сейчас работать надо.
вот это:
вот это: http://blog.lexa.ru/2011/12/15/o_numerologii.html#comment-22089
+ то что Макс пишет